The R-version of what we did in Introduction to useful functions in Excel

MVEN10

Author

Ullrika Sahlin

Preparations

Load packages

library(readr)
library(dplyr)
library(ggplot2)

Load data and save the variable to an object called x

df = as_tibble(read_csv("../data/breast-cancer.csv"))%>% select(radius_mean)

Descriptive statistics

summary(df)

  radius_mean    
 Min.   : 6.981  
 1st Qu.:11.700  
 Median :13.370  
 Mean   :14.127  
 3rd Qu.:15.780  
 Max.   :28.110

x = df$radius_mean
quantile(x,probs=0.25)

 25% 
11.7

median(x)

[1] 13.37

quantile(x,probs=0.95)

   95% 
20.576

mean(x)

[1] 14.12729

sd(x)

[1] 3.524049

min(x)

[1] 6.981

max(x)

[1] 28.11

length(x)

[1] 569

Calculate the three summary statistics described in the green area of the sheet.

The third quartile in the sample, P75

quantile(x,probs=0.75)

  75% 
15.78

The 5% quantile (or 5th percentile), P05

quantile(x,probs=0.05)

    5% 
9.5292

The coefficient of variation is the ratio between the sample standard deviation and the sample mean

sd(x)/mean(x)*100

[1] 24.94497

Histogram

hist(x)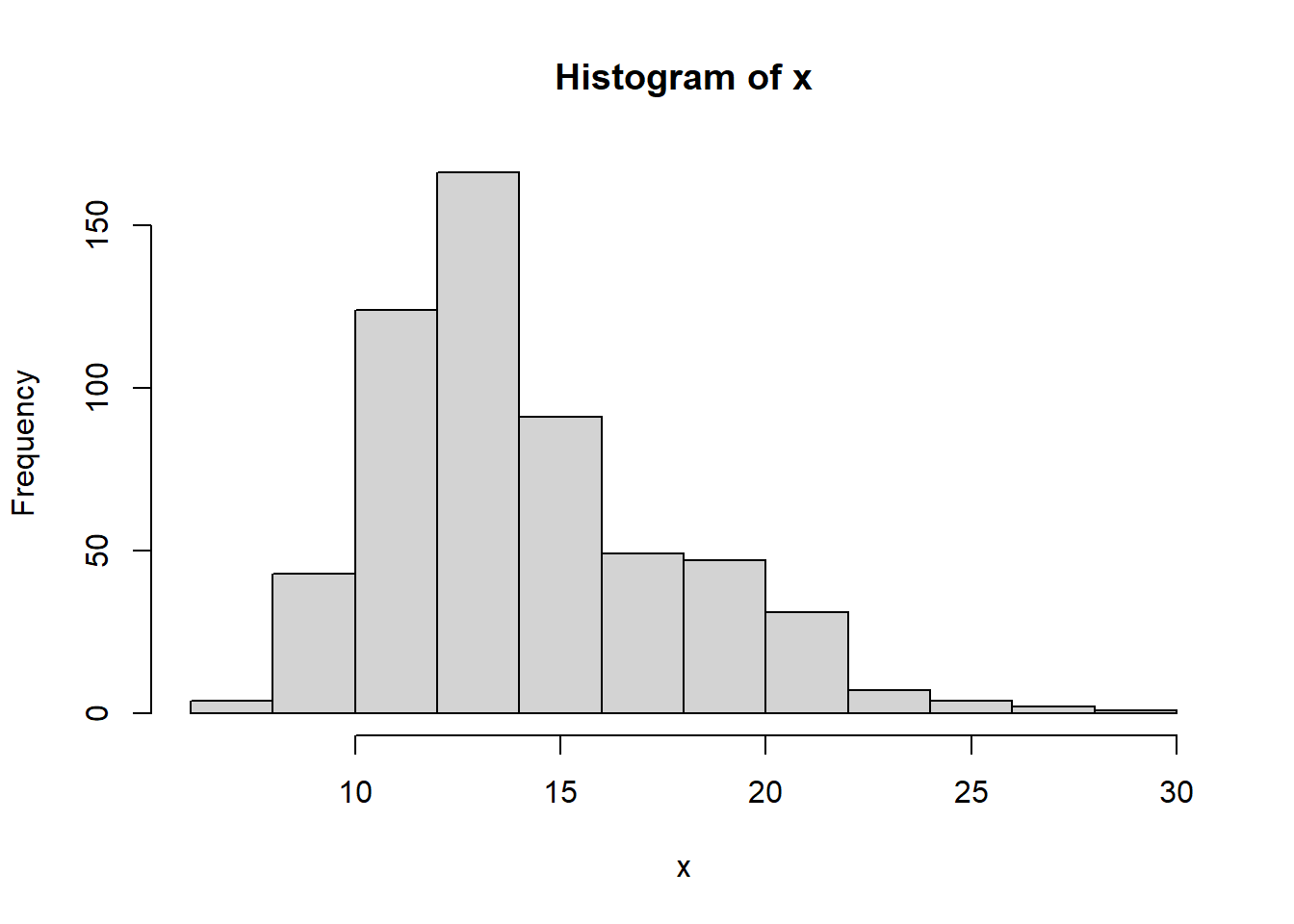

df %>% 
  ggplot(aes(x=x))+
  geom_histogram()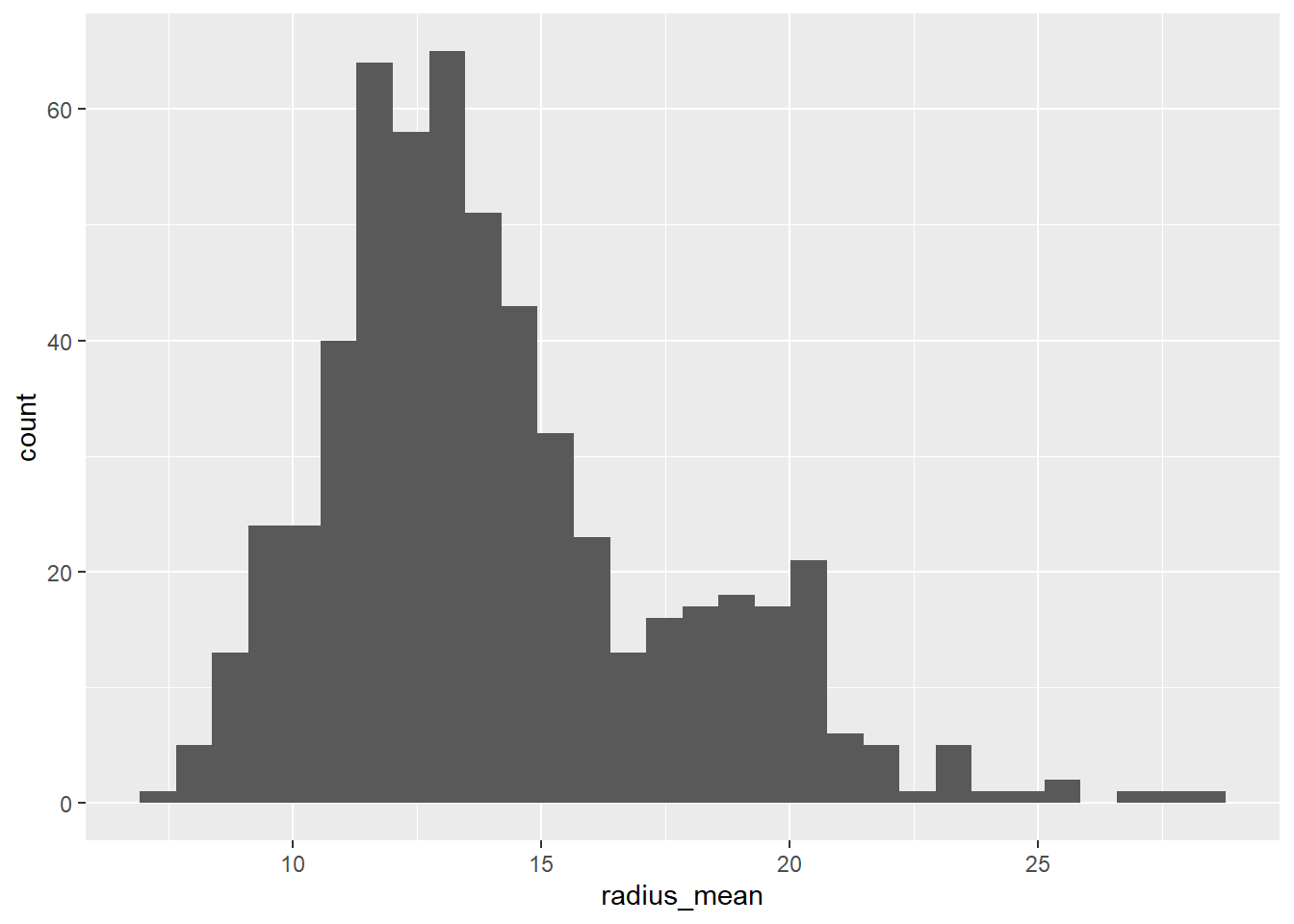

df %>% 
  ggplot(aes(x=x))+
  geom_histogram(binwidth = 2.5)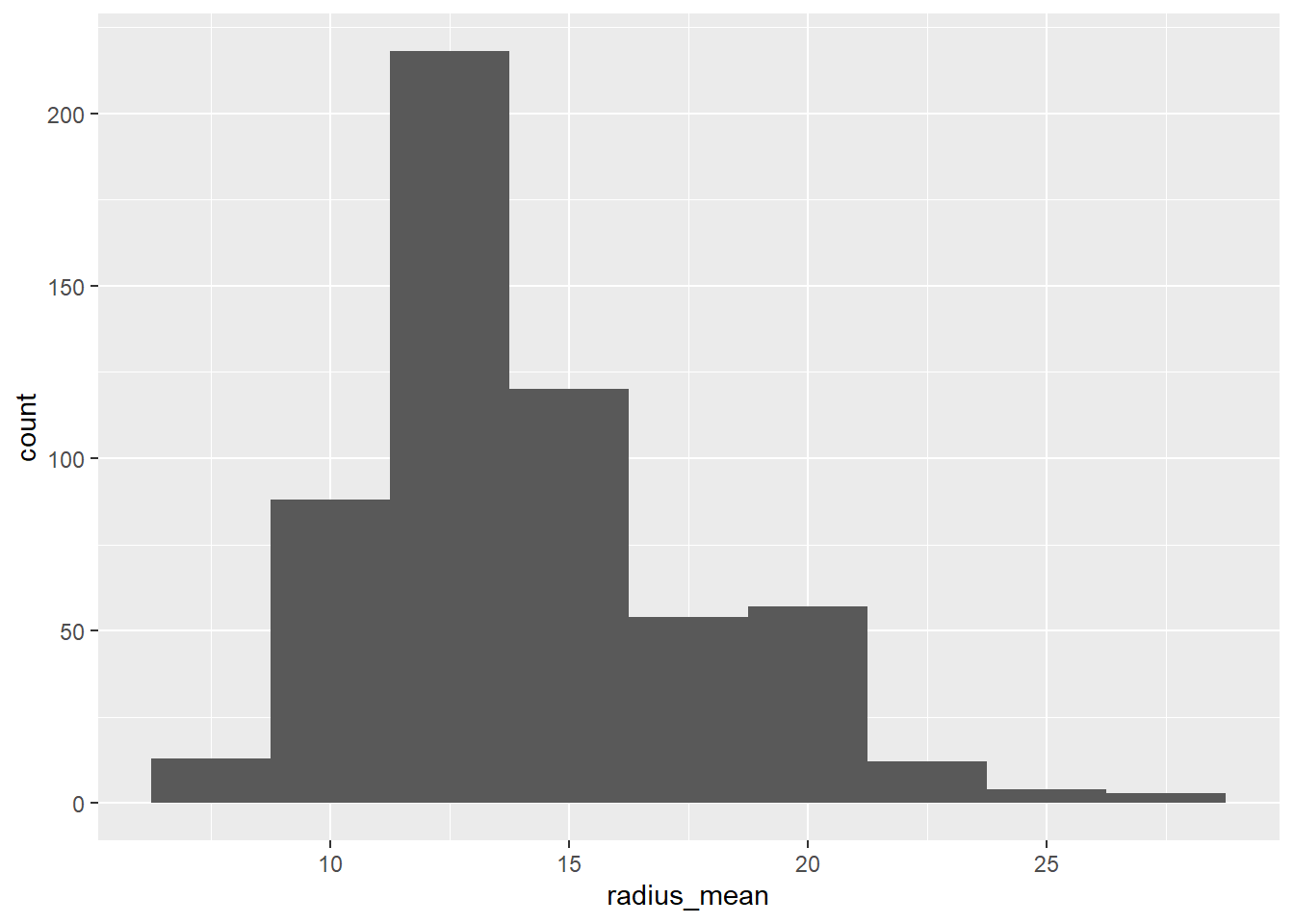

df %>% 
  ggplot(aes(x=x))+
  geom_density()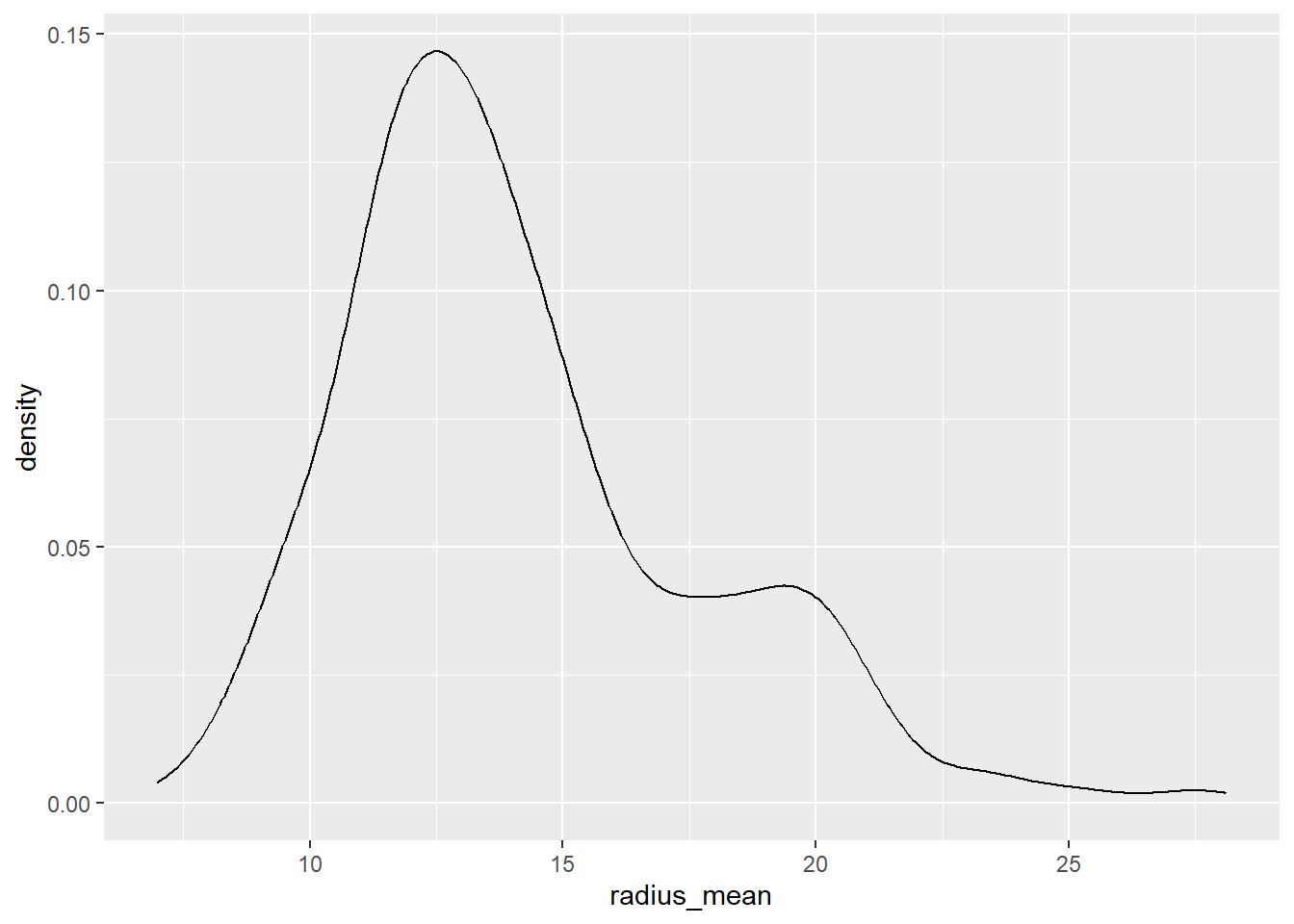

Probability functions

The probability functions follow the principles of combining p, d, q and r with the name (or short name) of the probability distributions.

Functions for the normal distribution
What to calculate	R-function
CDF	pnorm
PDF	dnorm
quantile	qnorm
random draw	rnorm

Calculate the probability that a normally distributed variable with mean 14 and standard deviation 3.5 is less than 10

pnorm(10,mean=14,sd=3.5)

[1] 0.126549

Find the 95% quantile in the same distribution

qnorm(0.95,mean=14,sd=3.5)

[1] 19.75699

Calculate the probability that an exponentially distributed variable with mean 14 is less than 10

pexp(10,rate=1/14)

[1] 0.5104583

Tip

Type a question mark before the function to see the help text ?pexp

Plot probability distributions

m=14
s=3.5
data.frame(pp=ppoints(100)) %>%
  mutate(x=qnorm(pp,m,s)) %>%
  mutate(d=dnorm(x,m,s)) %>%
  ggplot(aes(x=x,y=d))+
  geom_line()+
  xlab('value')+
  ylab('density')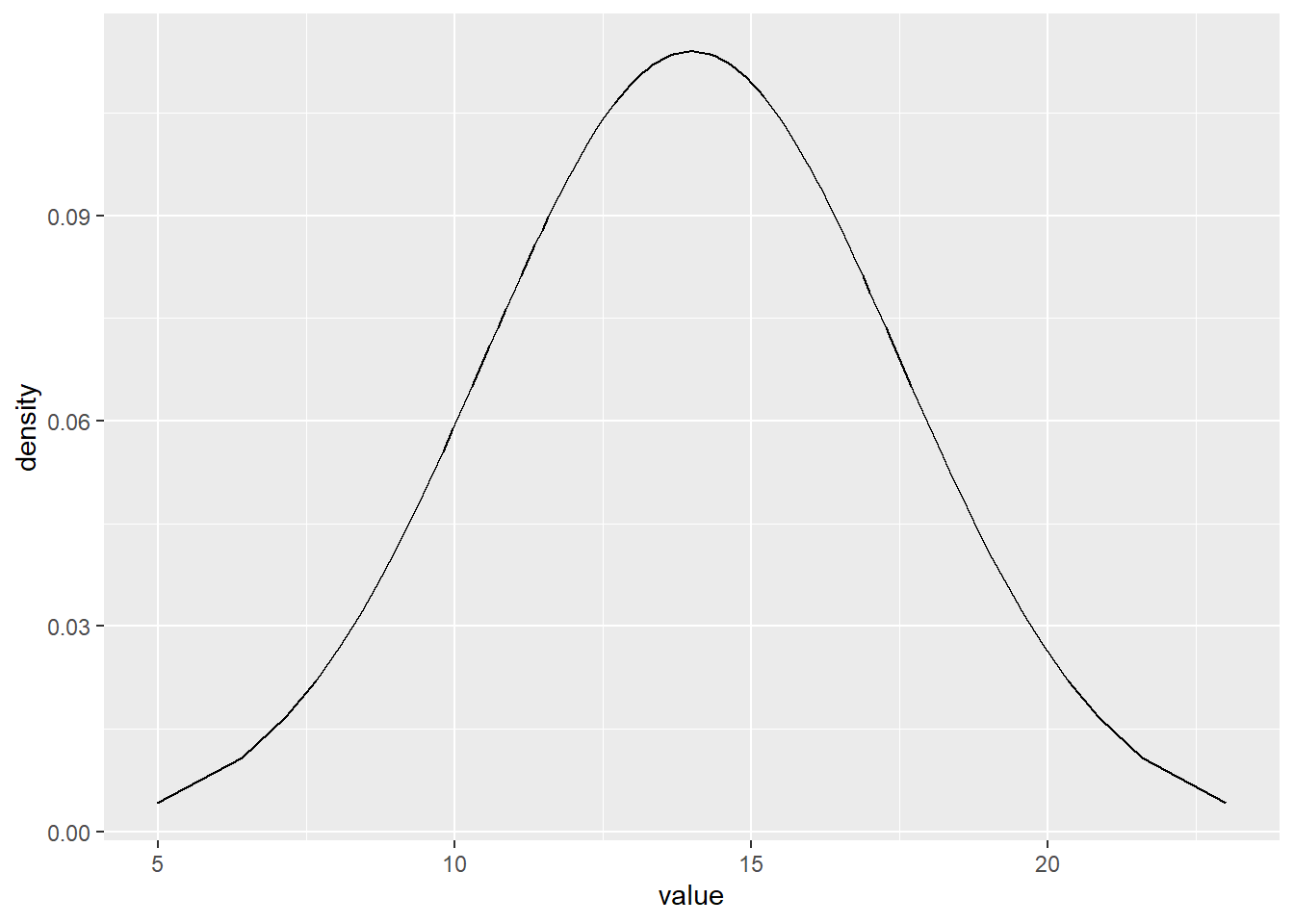

Extra

If you feel you have the time or do another time:

Copy the sheet and refine the grid by using pp-values from 0.001 to 0.999.

m=14
s=3.5
data.frame(pp=ppoints(1000)) %>%
  mutate(x=qnorm(pp,m,s)) %>%
  mutate(d=dnorm(x,m,s)) %>%
  ggplot(aes(x=x,y=d))+
  geom_line()+
  xlab('value')+
  ylab('density')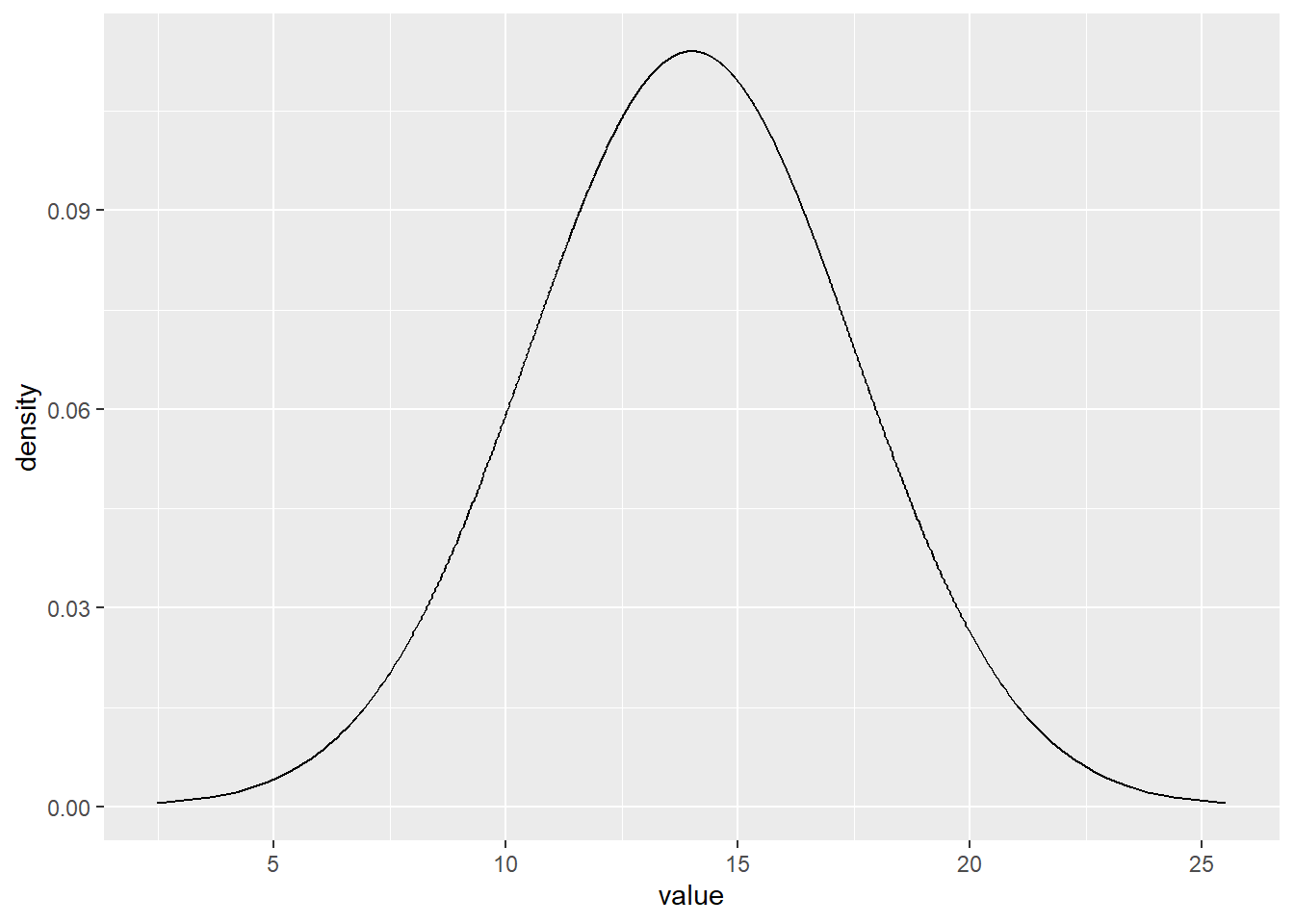

Random sampling

All sample generators start with a random number between 0 and 1. This is also a sample from a uniform distribution.

runif(1)

[1] 0.9704786

Type a function that generates a uniform random number in the interval 1 to 6.

runif(1,min=1,max=6)

[1] 5.595887

A random draw from a probability distribution can be generated by the inverse method. - Draws pp-values from a uniform distribution between 0 and 1 - Transform them into quantiles of the target distribution

Generates random draws from a normal distribution using the inverse method

qnorm(runif(1),m,s)

[1] 13.14799

This is already implemented as a function

rnorm(1,m,s)

[1] 18.37606

Draw from a beta distribution with parameters \(\alpha=2\) and \(\beta=8\)

rbeta(1,2,8)

[1] 0.2157914

Compare descriptive statistics against theoretical values

Wow - now we can generate data where we know the true value on parameters and all theoretical probabilities and quantiles, and compare with what we get when deriving descriptive statistics from the random sample.

This sheet generates a random sample of size 20 from a beta distribution.

rbeta(n=20,2,8)

 [1] 0.21436125 0.24865058 0.07527012 0.05475960 0.17566076 0.05934510
 [7] 0.25065048 0.05348027 0.33044344 0.23641477 0.08971576 0.17476356
[13] 0.19743103 0.15513189 0.45292185 0.03770521 0.27509703 0.04703781
[19] 0.19567211 0.18022758

A beta distribution has two parameters \(\alpha\) and \(\beta\)

The expected value of a beta distributed variable is \(\frac{\alpha}{\alpha+\beta}\)

Compare the calculated sample average to the theoretical expected value

alpha=2
beta=8
alpha/(alpha+beta)

[1] 0.2

mean(rbeta(n=20,alpha,beta))

[1] 0.1860472

We can also derive the theoretical quantile, let us say the P95.

Compare the quantile from the sample with the quantile calculated from the inverse probability distribution function

qbeta(0.95,alpha,beta)

[1] 0.4291355

quantile(rbeta(n=20,alpha,beta),probs=0.95)

      95% 
0.4128793

Which of them has the smallest difference? Why do you think it is like that?

Extra

If you feel you have the time or do another time:

Explore what happens with the difference between theoretical and statistical values when you increase sample size from 20 to a high number (close to 1000)?

Below I wrte a script where sample size is controlled at one place. The P95 is approximated fairly well by the sampling when I use \(n=10 000\).

alpha=2
beta=8
n=10000
alpha/(alpha+beta)

[1] 0.2

mean(rbeta(n=n,alpha,beta))

[1] 0.200594

qbeta(0.95,alpha,beta)

[1] 0.4291355

quantile(rbeta(n=n,alpha,beta),probs=0.95)

      95% 
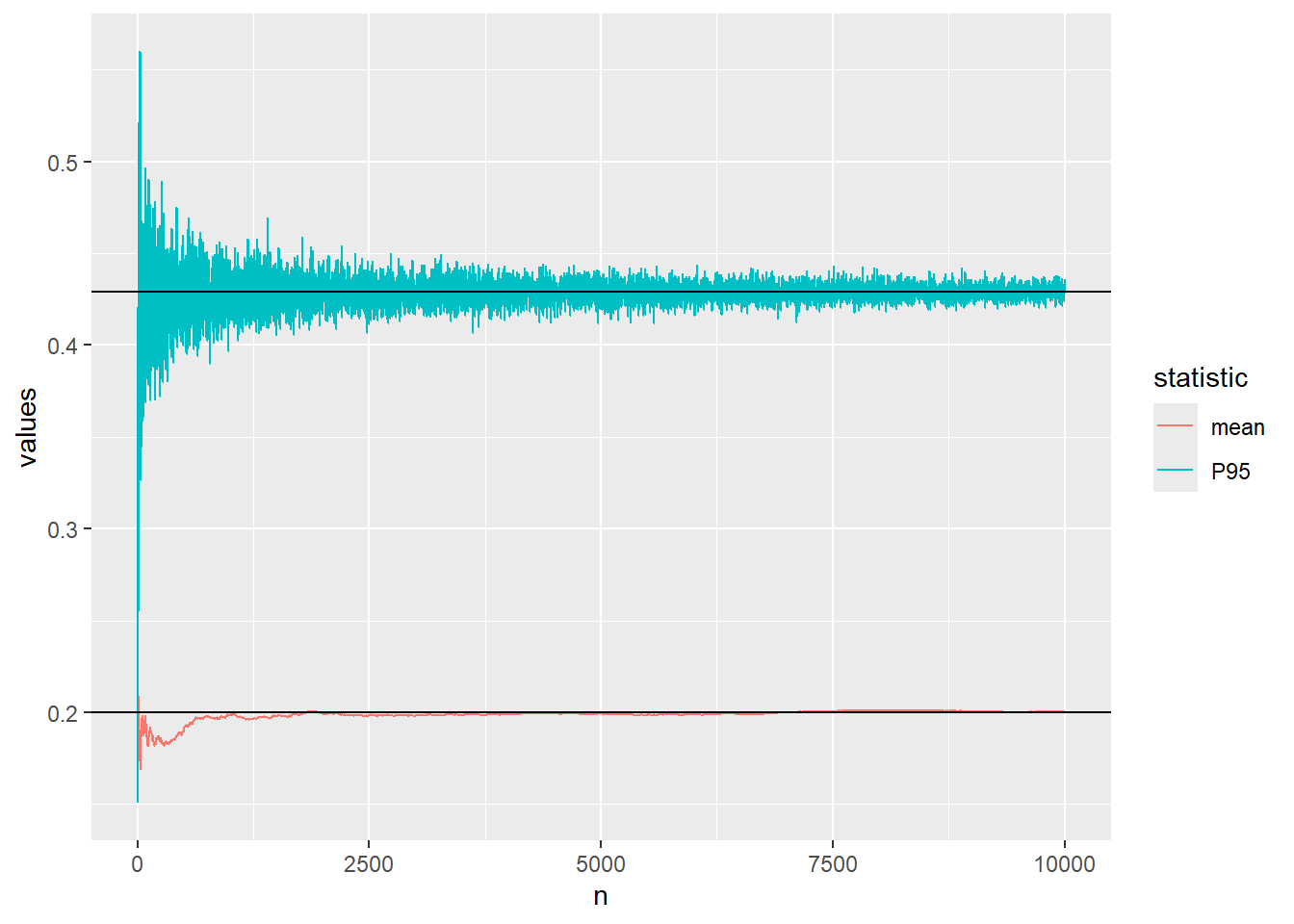
0.4327183

Let us visualise the convergence of the approximation of the mean and 95th percentile of the beta distribution using Monte Carlo simulation.

The code below defines a function which calculates the mean and P95 after every increase of the sample size and plots the convergence.

plot_conv <- function(n){
sample_mean=cummean(rbeta(n=n,alpha,beta))
sample_P95=unlist(lapply(1:n,function(iter){
  quantile(rbeta(n=iter,alpha,beta),probs=0.95)}))
data.frame(values=c(sample_mean,sample_P95),n=rep(1:n,2), statistic=rep(c("mean","P95"),each=n))  %>%
  ggplot(aes(x=n,y=values,color=statistic))+
  geom_line()+
  geom_hline(yintercept = alpha/(alpha+beta)) +
  geom_hline(yintercept = qbeta(0.95,alpha,beta))
}

We start with \(n=10\)

plot_conv(n=10)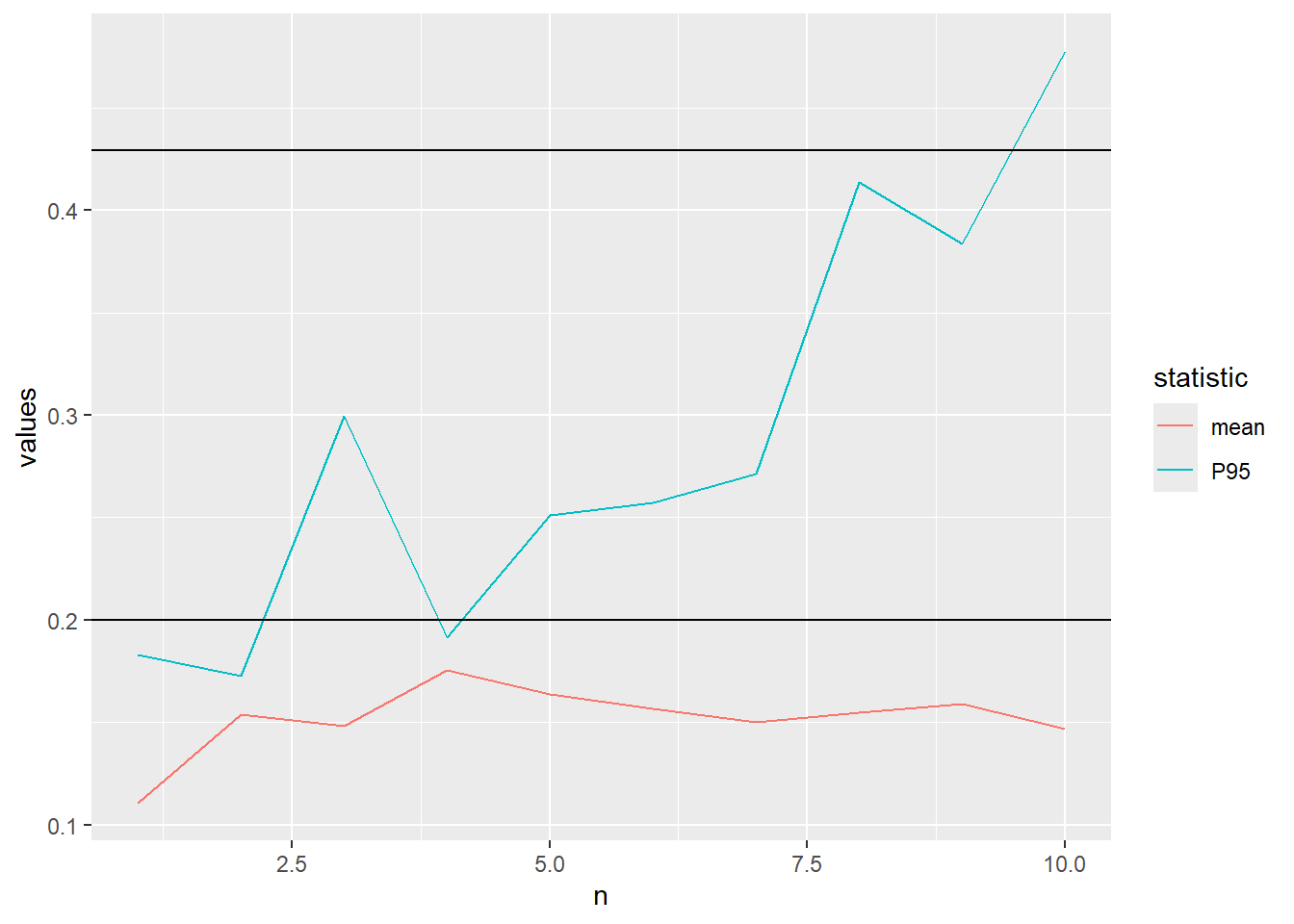

..increase to \(n=100\)

plot_conv(n=100)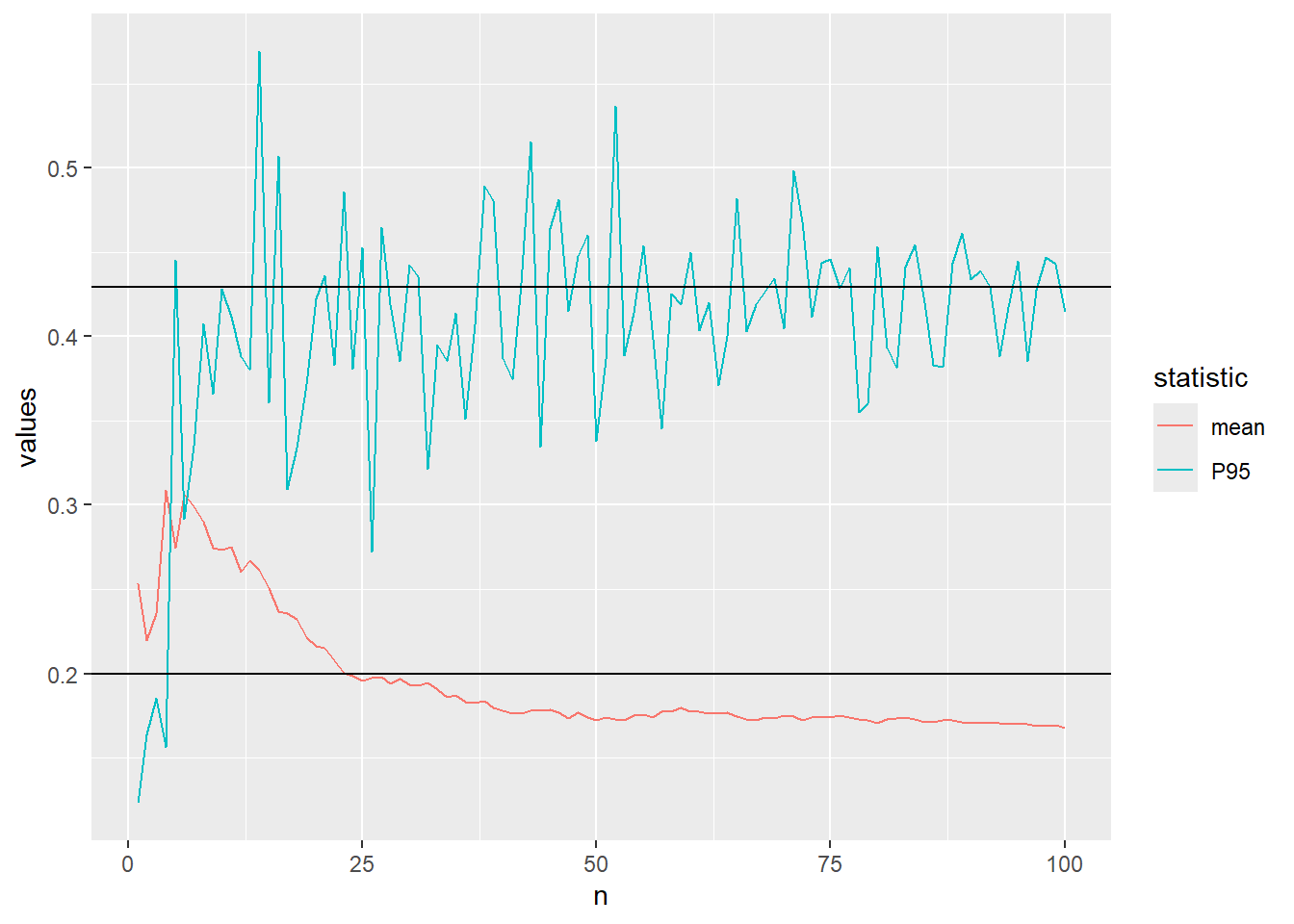

..increase to \(n=1000\)

plot_conv(n=10^3)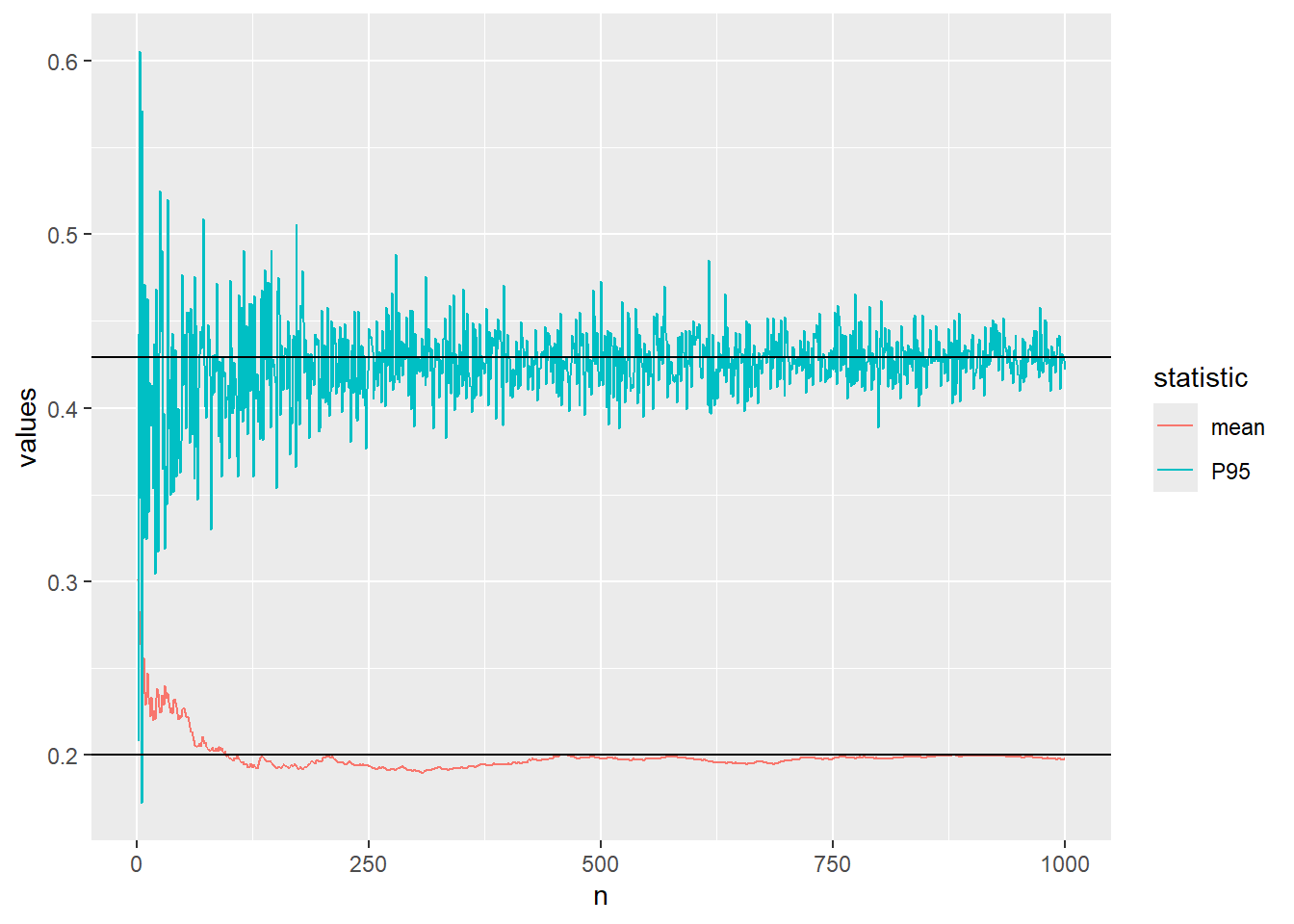

..and finally \(n=10000\)

plot_conv(n=10^4)